The search for a “Great Equilibrium”
So far, we’ve begun establishing a framework through which to look at intra-state power dynamics. We’ve seen how routes can be affiliated and gave a name to routes with the same destination – congruent. In addition, we’ve assigned destinations within the same route as harmonious. The analogy we’ve used was a car with occupants, sent out by tribe members. For now, we’ll disregard the method by which the number of occupants is chosen and the threshold for becoming an occupant, though it is crucial.
This just builds on the foundation of game theory work done by Nash, Arrow and others.
If you’d like to read more:
To create this primitive model we’ll also disregard for now tribe members with influence unproportional to their portion of the population.
Assuming that all the tribe members and their representatives view the world through bounded rationality, let’s test some initial assumptions:
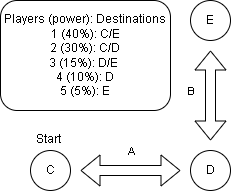
Assumption 1: Two Occupants with congruent destinations will always agree on at least 1 route until that destination is achieved.
Verdict: False
Exception 1: All possible routes pass through at least 1 destination which will empower or weaken the occupants in relation to each other or the other occupants.
Exception 2: The occupants are in the minority and know that while the route could reach their destination, it wouldn’t, given the other occupants’ destinations.
Here we can see that occupant 1 is ambivalent between destinations C and E, the same is true for occupant 2 and destinations C and D, and occupant 3 with destinations D and E, the starting position is C. We can see that D is a congruent destination for occupants 2. 3 and 4, which comprise a majority. But destination D is unstable because if reached, both regressing to C and advancing to E have a majority, and a larger majority isn’t a guarantee for choosing that destination. Occupant 1 is ambivalent, but path dependency comes into play he wants to avoid D, leading to remaining stable at C.
So here: Occupants 3, 4, and 5 will push for D, Occupant 2 will push to remain at C (even though his destination D is congruent with 3 and 4) and Occupant 1 will also push to remain at C.
Assumption 2: Two occupants with at least 1 harmonious route and a majority will always agree on 1 route until they are no longer harmonious.
Verdict: False
In our example, occupants 1 and 2 are harmonious in their route to D since it can lead to E, but once reached the car might be stuck at D, since it would also have a majority. Therefore, occupant 1 wouldn’t risk getting stuck there and would disagree with this route. Each destination has a majority, and once one is reached – it will not be changed while occupants’ goals are the same.
Rule #2: First Majority Stability
If:
- A majority of power agrees on a destination
And:
- It is reached
And:
- That same make up of majority isn’t in favor of a different destination
Then:
- The car will remain stationary at the initially reached destination.
Journey Fright
We can see that while we all might want to get to a similar destination, we are afraid to start going there and get stuck halfway, to become victims of our ambition. While no person is truly ambivalent between 2 destinations – I believe this model can be a rough approximation and help us devise strategies.
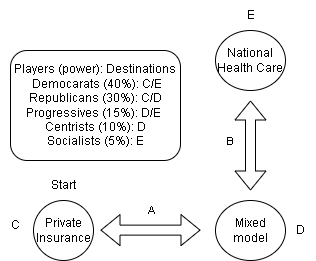
While the percentages are off and the nature of group names here is arbitrary, we can take the U.S. as an example. We see that while each of the options mentioned has majority support – the first majority was in place for a long time, it all depends on the starting point. America did transition to a mixed model, possibly due to changes in the support for different destinations
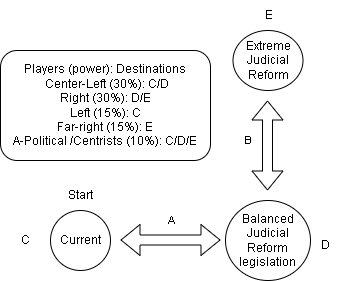
I’m adding a rough approximation of the power balance concerning Israel’s judicial reform as it currently rules the news cycle here and displays similar dynamics.
What we learn from this is that it’s not enough to have a majority – you have to get to your destination first.

Leave a comment